12月10日出版的国际顶级学术期刊《Nature》发表了我院博士毕业生杨倩(现为英国曼彻斯特大学博士后)为第一作者的文章Capillary condensation under atomic-scale confinement (Nature, 2020, 588, 250–253 , https://doi.org/10.1038/s41586-020-2978-1),报道了纳米限域毛细凝聚新理论,并对传统开尔文公式进行了修正,使其能够更好地描述亚纳米尺度的毛细凝聚现象,为解开毛细凝聚这一百年谜题提供了方案。材料科学与工程公司(材料先进技术教育部重点实验室)教授、前沿科学技术研究院经理周祚万博士为该文章的共同作者。

毛细凝聚,是我们从教科书中学到的自然现象,通常在接触表面或多孔材料中发生,在我们生活中处处存在,会影响包括摩擦、吸附、润滑、腐蚀等在内的诸多重要性质,也在微加工技术、医药、食品加工等许多工业技术过程中发挥着重要作用,就连小孩子们在沙滩上玩耍堆砌的沙堡,也离不开毛细凝聚。毛细凝聚现象通常由开尔文方程进行科学描述,该方程提出距今已有150余年,能很好地解释在大于10 nm通道中的毛细凝聚现象,这个宽度只有人头发丝的千分之一。然而若想要毛细凝聚发生在环境湿度条件(通常是相对湿度30-50%) 下,通常需要更小(<1 nm) 的通道尺寸,而这个尺寸跟水分子自身大小(大约0.3 nm)相当。在这种情况下,自发凝聚的通道中便只能容纳几层水分子,显然宏观开尔文方程不能继续用于阐述该尺寸下的毛细凝聚现象。实际上,在该尺度下开尔文方程甚至不再具有意义,例如当只有几层水分子存在时,我们无法定义水半月板的曲率半径这一开尔文方程中的重要参数。但长期以来,用于验证开尔文方程适用性的体系受限于表面粗糙度等实验问题难以建立,因此,即使开尔文方程的适用性虽并未得到完全证明,却依然在被大家广泛使用。
来自曼彻斯特的研究者们通过长时间的努力,采用具有原子级别光滑表面的云母和石墨二维晶体,通过将具有一定原子层数的二维晶体堆叠在两层晶体间,得到了具有原子级别光滑表面的纳米通道,最小的通道只有1个原子层高度,只能容纳一层水分子。该工作证明即使在这样最小的通道里,开尔文方程依旧适用。这是一个很意外的结果,甚至和我们的认知相违背,因为在这么小的维度里,连水分子的结构都是离散的层状结构。“这对我来说很意外,我们期望的是传统理论失效”本文的第一作者杨倩博士说到,“但这个有着百年历史的方程居然依旧成立”;她提到,开尔文方程这种良好的适用性,也同样是偶然的。在发生毛细凝聚的纳米通道中通常会产生超过1000个大气压的负压,超过深海海底的压力,如此巨大的压力可以使通道发生埃 (1埃 = 0.1 nm) 级别的尺寸调整,而这就能够使通道只容纳整数层水分子。正是由于这样的细微调整,使得开尔文方程具有了在该尺度下的广泛适用性。
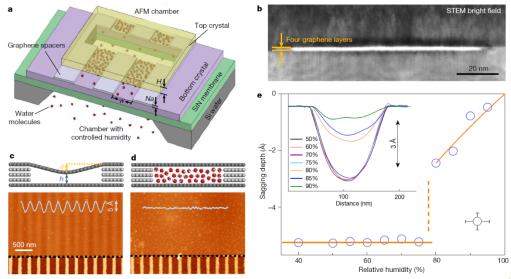
“好的理论通常都有这样的特性,能在适用范围外依旧合理”,文章通信作者、诺贝尔物理奖得主、公司荣誉教授A. K. Geim博士说到,“开尔文勋爵是伟大的科学家,有许多重大发现,但即使他看到这样的结果可能也会感到惊奇,毕竟他最早的实验是建立在毫米级别尺度下的。但实际上,他也曾预言这是不可能的。所以,我们的工作能同时证明开尔文既是正确,也是不正确的”。
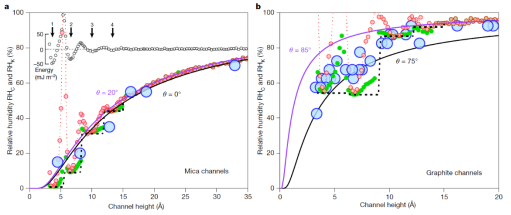
近年来,周祚万教授领衔的公司功能高分子材料研究团队瞄准前沿科学和交叉领域,开展探索研究,并积极拓展国际合作渠道,鼓励研究生同学特别是博士研究生勇于创新,敢于突破,走有特色的国际化前沿学术创新之路。据最近发布的“ESI高被引论文”统计数据,该研究团队共有9篇文章入选,总数居全校之首。此外,课题组研制的载人航天舱内抗菌材料已成功应用于天宫等系列装备的相关科学试验,并支撑我国空间站研制过程中的抗菌材料选型和微生物防护技术体系,相关成果获得2019年四川省科技进步一等奖。